CÓDIGOS

Código BCD. Decimal codificado en Binario

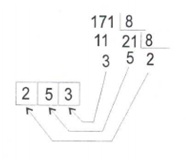
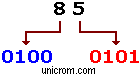
El código BCD utiliza 4 dígitos binarios (ver en los dos ejemplos que siguen) para representar un dígito decimal (0 al 9). Cuando se hace conversión de binario a decimal típica no hay una directa relación entre el dígito decimal y el dígito binario.

Ejemplo 1: Conversión directa típica entre un número en decimal y uno binario. 8510 = 10101012. La representación el mismo número decimal en código BCD se muestra a la derecha.

Código Gray

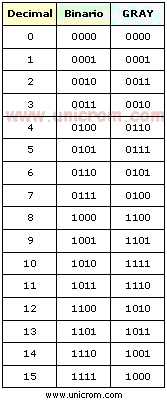
El código Gray es un tipo especial de código binario que no es ponderado (los dígitos que componen el código no tienen un peso asignado). Su característica es que entre una combinación de dígitos y la siguiente, sea ésta anterior o posterior, sólo hay una diferencia de un dígito.

Por eso también se le llama Código progresivo. Esta progresión sucede también entre la última y la primera combinación. Por eso se le llama también código cíclico.

Exceso de 3

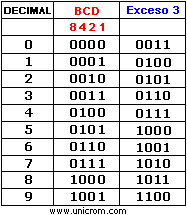
El código Exceso 3 se obtiene sumando “3” a cada combinación del código BCD natural. Ver la tabla inferior. El código exceso 3 es un código en donde la ponderación no existe (no hay “pesos” como en el código BCD natural y código Aiken). Al igual que el código Aiken cumple con la misma característica de simetría. Cada cifra es el complemento a 9 de la cifra simétrica en todos sus dígitos.

Código ASCII "American Standard Code for Information Interchange" (Código Standard Norteamericano para Intercambio de Información)

El ASCII es un código numérico que representa los caracteres, usando una escala decimal del 0 al 127. Esos números decimales son convertidos por la computadora en números binarios para ser posteriormente procesados. Por lo tanto, cada una de las letras que escribas va a corresponder a uno de estos códigos.

Código ASCII: 32 ESPACIO 

Código ASCII: 33 !

Código ASCII: 34 “

Código ASCII: 35 #

Código ASCII: 36 $

Código ASCII: 37 %

Código ASCII: 38 &

Código ASCII: 39 ‘

Código ASCII: 40 (

Código ASCII: 41 )

Código ASCII: 42 *

Código ASCII: 43 +

Código ASCII: 44 ,

Código ASCII: 45 -

Código ASCII: 46 .

Código ASCII: 47 /

Código ASCII: 48 0

Hasta el Código 57 son todos los números.

Código ASCII: 58 :

Código ASCII: 59 ;

Código ASCII: 60 <

Código ASCII: 61 =

Código ASCII: 62 >

Código ASCII: 63 ?

Código ASCII: 64 @

Código ASCII: 65 A

Hasta el código 90 son todas las letras mayúsculas.

Código ASCII: 91 | 

Código ASCII: 92 \ 

Código ASCII: 93 ] 

Código ASCII: 94 ^ 

Código ASCII: 95 _ 

Código ASCII: 96 ` 

Código ASCII: 97 a 

Hasta el 122 todas las letras minúsculas.

Código Paridad

Los códigos de paridad se usan en telecomunicaciones para detectar, y en algunos casos corregir, errores en la transmisión. Para ellos se añade en origen un bit extra llamado bit de paridad a los n bits que forman el carácter original.

Este valor del bit de paridad se determina de forma que el número total de bits 1 a transmitir sea par (código de paridad par) o impar (código de paridad impar).

Así, para el código de paridad par el número de unos contando el carácter original y el bit de paridad tiene que ser par. Por lo tanto, el bit de paridad será un 0 si el número total de unos a transmitir es par y un 1 para un número impar de unos.

Por el contrario, para el código de paridad impar el número de unos contando el carácter original y el bit de paridad ha de ser impar. De esta forma, el bit de paridad será un 0 si el número total de unos es impar y un 1 para un número par de unos.

Normalmente el bit de paridad se añade a la izquierda del carácter original.

Este método, aunque resulta satisfactorio en general, puede detectar sólo un número impar de errores de transmisión. Es decir, sólo es útil si los errores no cambian un número par de bits a la vez, ya que un número par de errores no afecta a la paridad final de los datos.

SISTEMAS NUMERICOS

SISTEMA DECIMAL

El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez. El conjunto de símbolos utilizado (sistema de numeración arábiga) se compone de diez cifras diferentes: cero (0); uno (1); dos (2); tres(3); cuatro (4); cinco (5); seis (6); siete (7); ocho (8) y nueve (9).

Excepto en ciertas culturas, es el sistema usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistema de numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método de el binario o el hexadecimal.

EJEMPLO:

75.269 = 70.000 + 5.000 + 200 + 60 + 9 =

= 7x10.000 + 5x1.000 + 2x100 + 6x10 + 9

SISTEMA BINARIO

El sistema binario, en matemáticas e informática, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es el que se utiliza en las computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).

Ejemplo de secuencia de números del 0 al 7 en binario: 

0    0 

1    1 

10    2 

11   3 

100    4 

101    5 

110    6 

111    7

SISTEMA OCTAL

El sistema numérico en base 8 se llama octal y utiliza los dígitos 0 a 7.

Para convertir un número en base decimal a base octal se divide por 8 sucesivamente hasta llegar a cociente 0, y los restos de las divisiones en orden inverso indican el número en octal. Para pasar de base 8 a base decimal, solo hay que multiplicar cada cifra por 8 elevado a la posición de la cifra, y sumar el resultado.

Es más fácil pasar de binario a octal, porque solo hay que agrupar de 3 en 3 los dígitos binarios, así, el número 74 (en decimal) es 1001010 (en binario), lo agruparíamos como 1 / 001 / 010, después obtenemos el número en decimal de cada uno de los números en binario obtenidos: 1=1, 001=1 y 010=2. De modo que el número decimal 74 en octal es 112.

Por ejemplo, si deseamos representar ese mismo número decimal a base 8 (octal), sólo variará el número de base que constituye el dividendo: 

                                         

Aquí se puede ver una disminución en la cantidad de operaciones a realizar con respecto a la operación de pasar a binario. En este caso, se ha utilizado un sistema con más dígitos. Y para comprobar el resultado, volvemos a transformarlo a base decimal: 2538 = 2 x 82 + 5 x 81 + 3 x 80 = 2 x 64 + 5 x 8 + 3 x 1 = 128 + 40 + 3 = 17110

SISTEMA HEXADESIMAL

El sistema numérico hexadecimal o sistema hexadecimal (a veces abreviado como Hex, no confundir con sistema sexagesimal) es un sistema de numeración que emplea 16 símbolos. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria, según el teorema general de la numeración posicional, equivale al número en base 16 , dos dígitos hexadecimales corresponden exactamente —permiten representar la misma línea de enteros— a un byte.

Ejemplo de conversión del número 2031810 a hexadecimal: 

                                       

Comprobando el resultado: 4F5E16 = 4 x 163 + F x 162 + 5 x 161 + E x 160 = 4 x 163 + 1510 x 162 + 510 x 161 + 14 x 160 = 20.31810